课 题 | 同位角、内错角、同旁内角 | 第 周 | 第 课时 | ||
教 学 目 标 | 1.了解同位角、内错角、同旁内角的概念; 2.同位角、内错角、同旁内角的识别. | ||||
教学重难点 | 重点:能在复杂的图形中识别同位角、内错角、同旁内角. 难点:掌握同位角、内错角、同旁内角的特征,能正确识别图形中的同位角、内错角和同旁内角. | ||||
教学准备 | |||||
课时安排 | |||||
教 学 过 程 | |||||
一、创设情景 明确目标 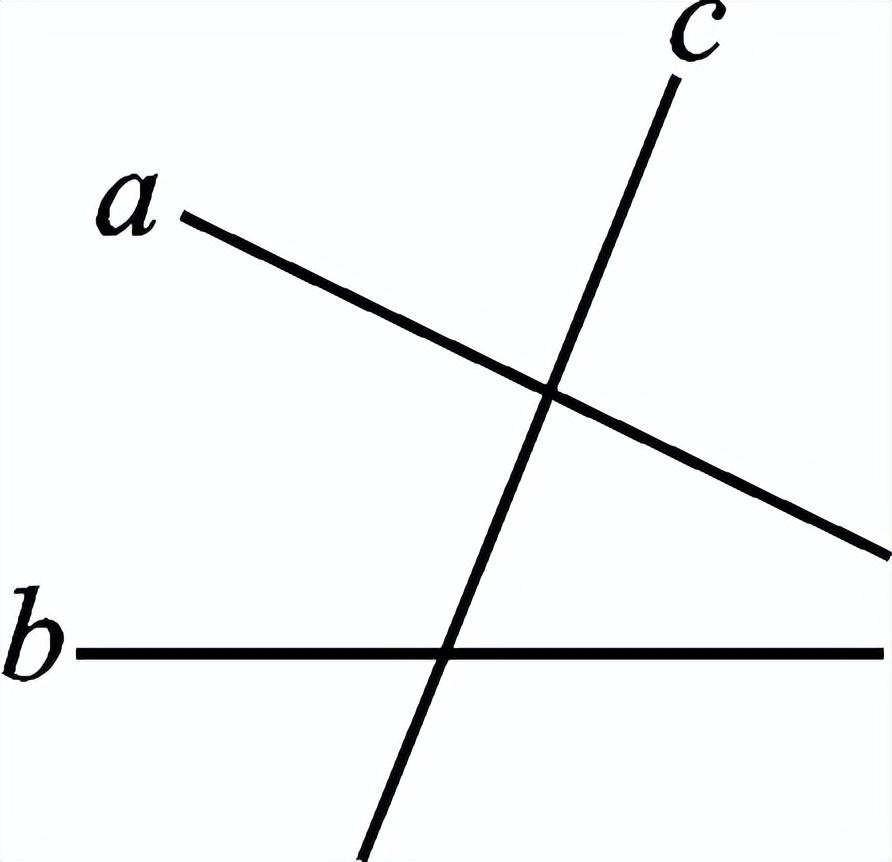 如图,将木条a,b与木条c钉在一起,木条在转动过程中,两个交点处共形成8个角,在不同顶点处各取一个角,则他们是对顶角吗?是邻补角吗?若都不是,那么它们是具有什么关系的角呢? 二、自主学习 指向目标 自学教材第6至7页,请完成学生用书部分. 1.两条直线被第三条直线所截,没有公共顶点的两个角的位置关系有__同位角__、__内错角__和__同旁内角__. 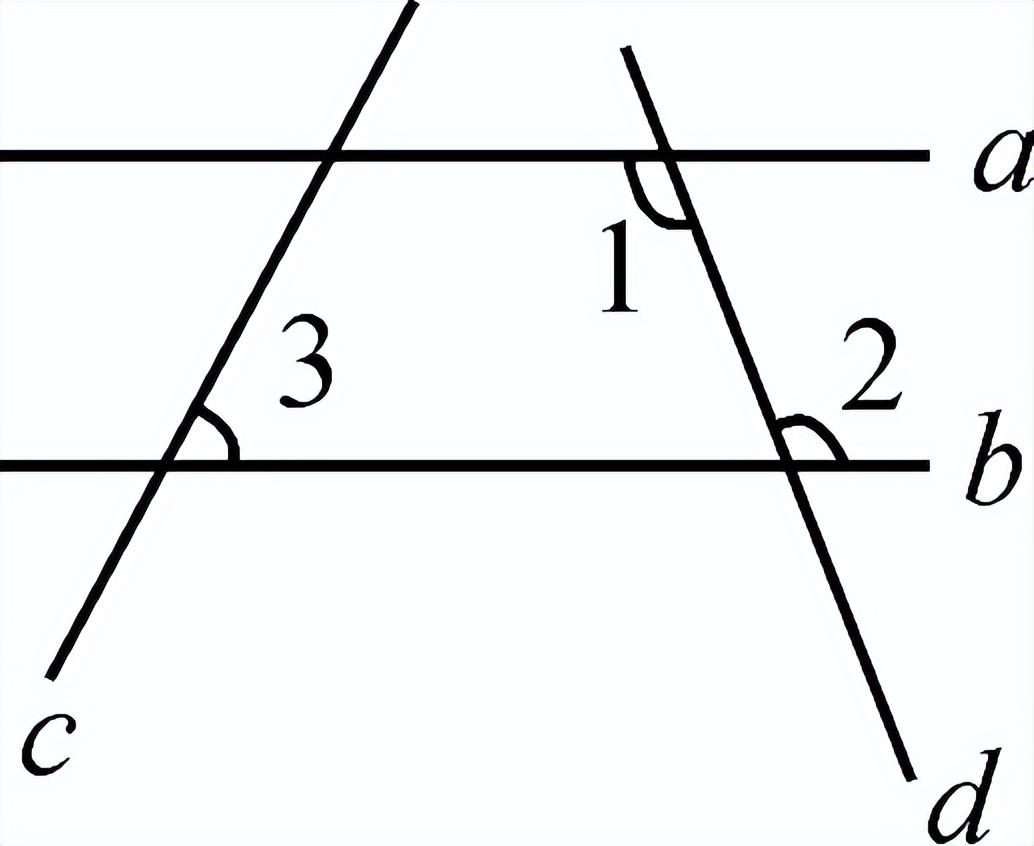 2.如图,∠1和∠2是直线__a__和__b__被直线__d__所截得的__内错角__;∠2和∠3是直线__c__和__d__被直线__b__所截得的__同位角__. 三、合作探究 达成目标 一 同位角、内错角、同旁内角的概念 活动1: (一)同位角 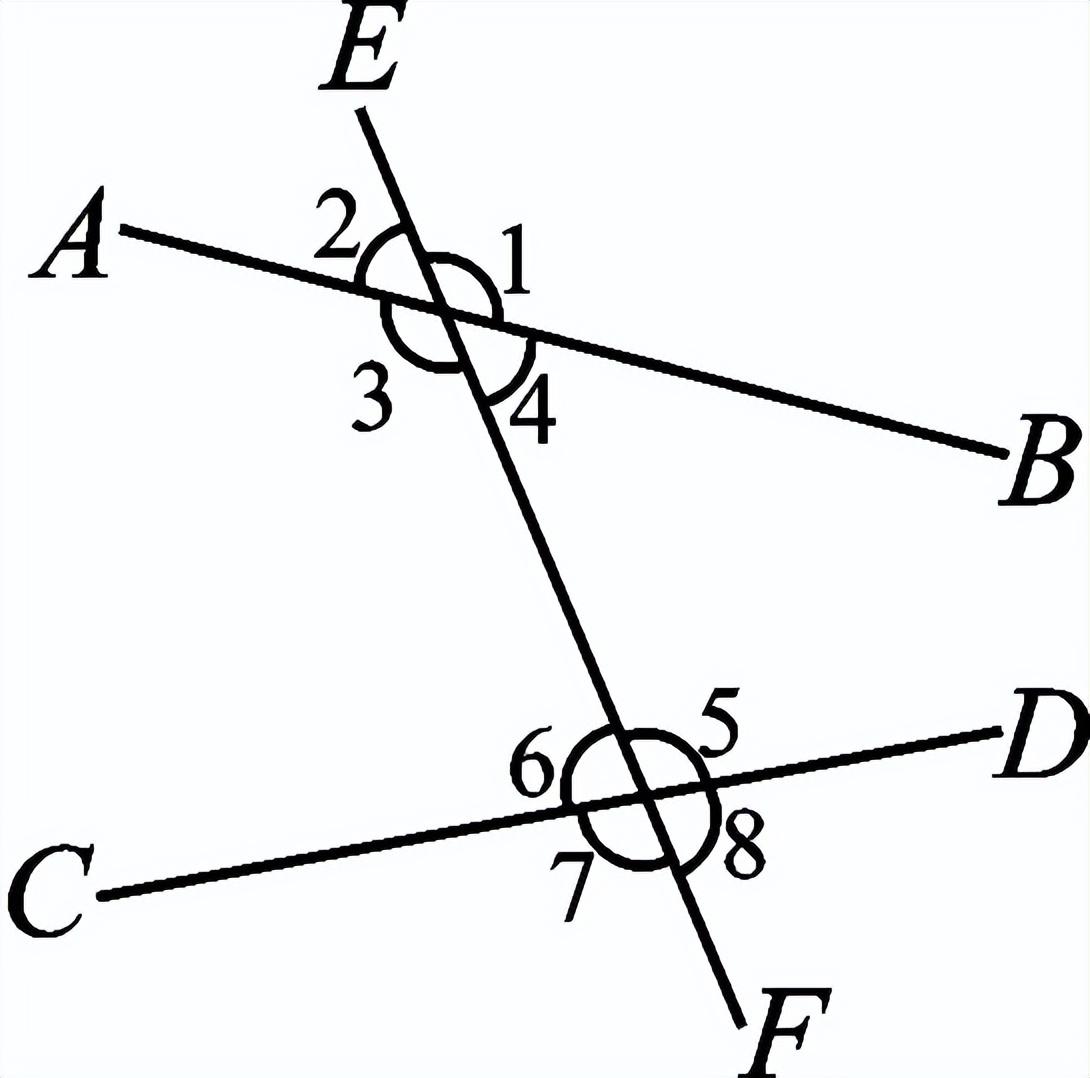 1.定义:如图,∠1和∠5,分别在被截两直线AB、CD的________,在截线EF的________.具有这种位置关系的一对角叫做同位角. 2.请你找出图中还有哪几对角构成同位角. 3.两条直线被第三条直线所截构成的八个角中,共有________对同位角. (二)内错角 1.定义:如上图,∠3和∠5,分别在被截两直线AB、CD的________,在截线EF的________.具有这种位置关系的一对角叫做内错角. 2.请你找出图中还有哪几对角构成内错角. 3.两条直线被第三条直线所截构成的八个角中,共有________对内错角. (三)同旁内角 1.定义:如图,∠3和∠6,分别在被截两直线AB、CD的________,在截线EF的________.具有这种位置关系的一对角叫做同旁内角. 2.请你找出图中还有哪几对角构成同旁内角? 3.两条直线被第三条直线所截构成的八个角中,共有________对同旁内角. 展示点评:产生同位角、内错角、同旁内角的前提条件是两条直线被第三条直线所截,它们的名称反映了两角之间的位置关系. 小组讨论:如何判断两个角是否具有同位角、内错角、同旁内角的关系? 反思小结:辨认同位角要注意位置上的两个“同”字,在截线的同旁,被截两直线的同方;辨认内错角要注意“内”“错”两字,在被截两直线之内,在截线的两旁,“错”是交错的意思;辨认同旁内角要注意“同”“内”两字,在截线的同旁,在被截两直线之内. 针对训练 1.教材第7页课后练习第1题. 2.下列图形中,∠1和∠2是同位角的是( B ) 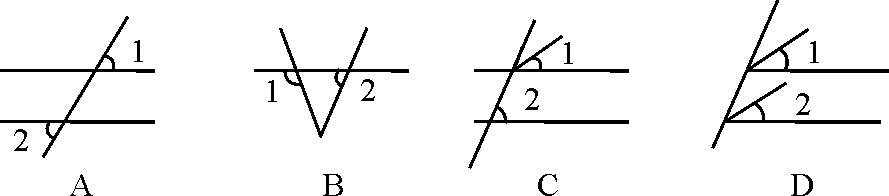 二 同位角、内错角、同旁内角的识别 活动2: 如图,直线DE、BC被直线AB所截. 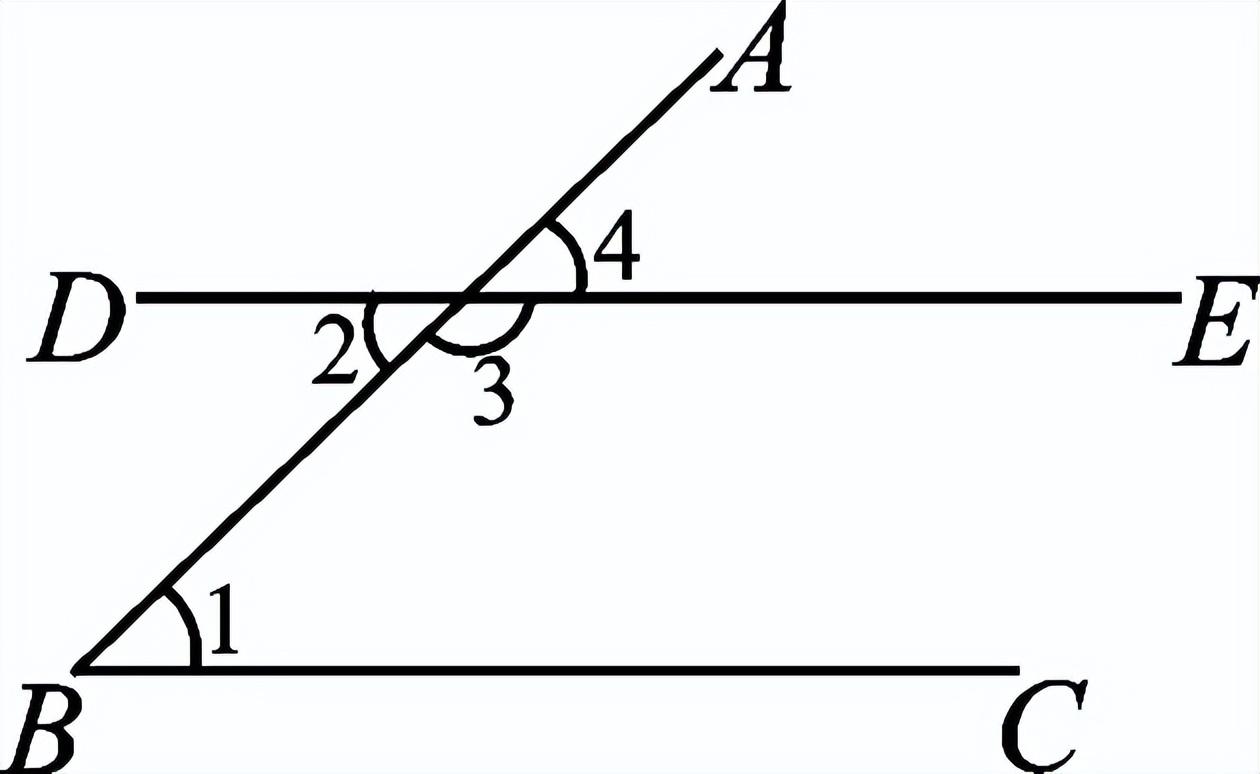 (1)∠1与∠2、∠1与∠3、∠1与∠4各是什么角? (2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么? (3)这三组角从位置上各有什么特征?它们分别在两被截直线和截线的什么地方?若把图形分离出来,各形如哪个字母? (4)∠2与∠4是具有什么位置关系的角?大小关系如何? (5)∠3和∠4是具有什么位置的角?大小关系又如何? 展示点评:如果∠1=∠4,则∠1=∠2;如果∠4与∠3互补,那么∠1与∠3也互补. 小组讨论:同位角、内错角、同旁内角各有什么特征? 反思小结:同位角、内错角、同旁内角的特征:“三线八角”;同位角:“F”字形,“同旁同侧”;内错角:“Z”字形,“之间两侧”;同旁内角:“U”字形,“之间同侧”. 针对训练 3.教材第7页练习第2题. 4.如图,∠1和∠2是两条直线__AD、BC__被直线__BD__所截而成__内错__角,∠A和∠3是两条直线__AD、BC__被直线__AB__所截而成的__同位__角;∠C和∠ABC是两条直线__AB、CD__被直线__BC__所截而成的__同旁内__角. 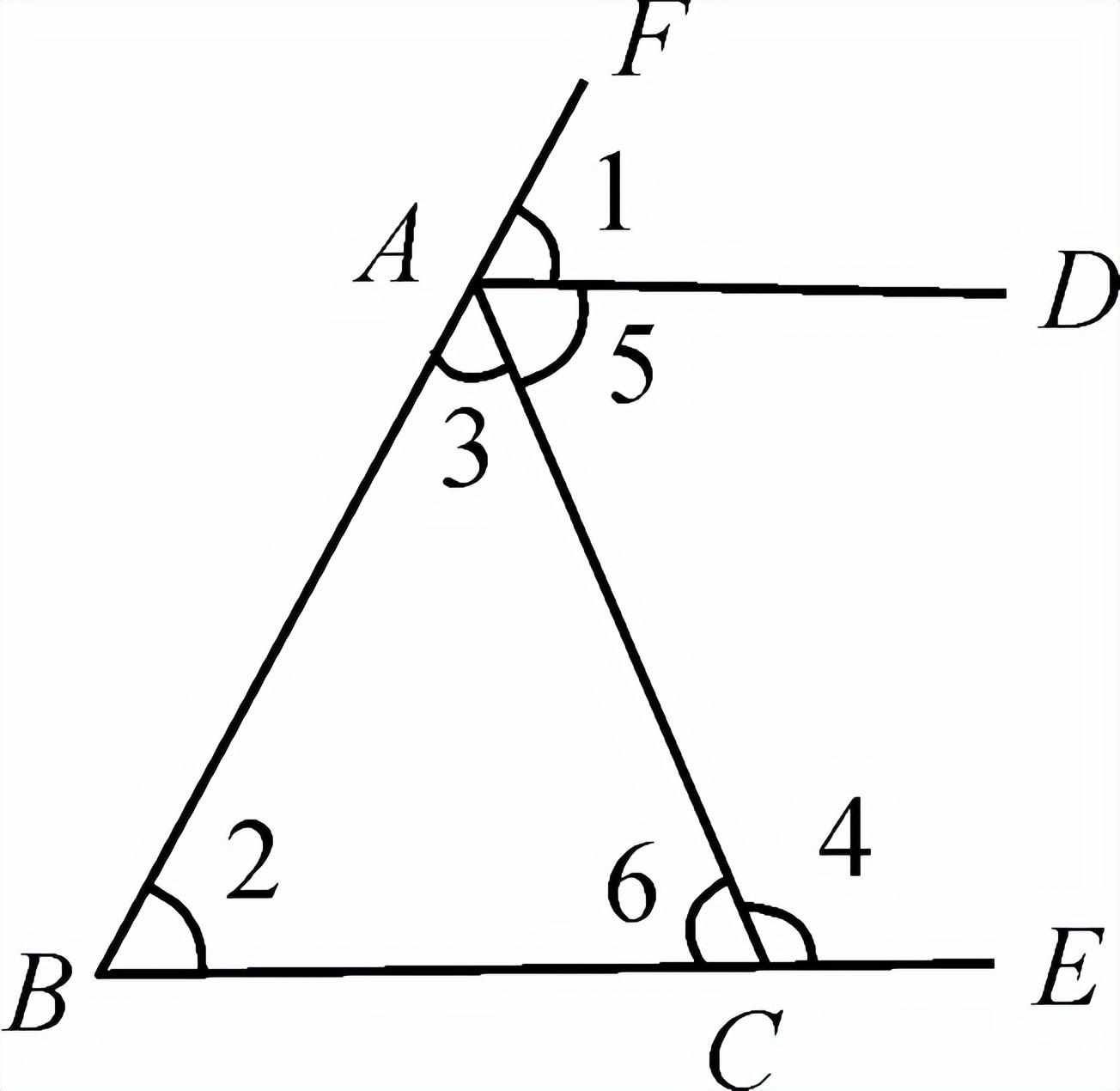 ,第5题图) 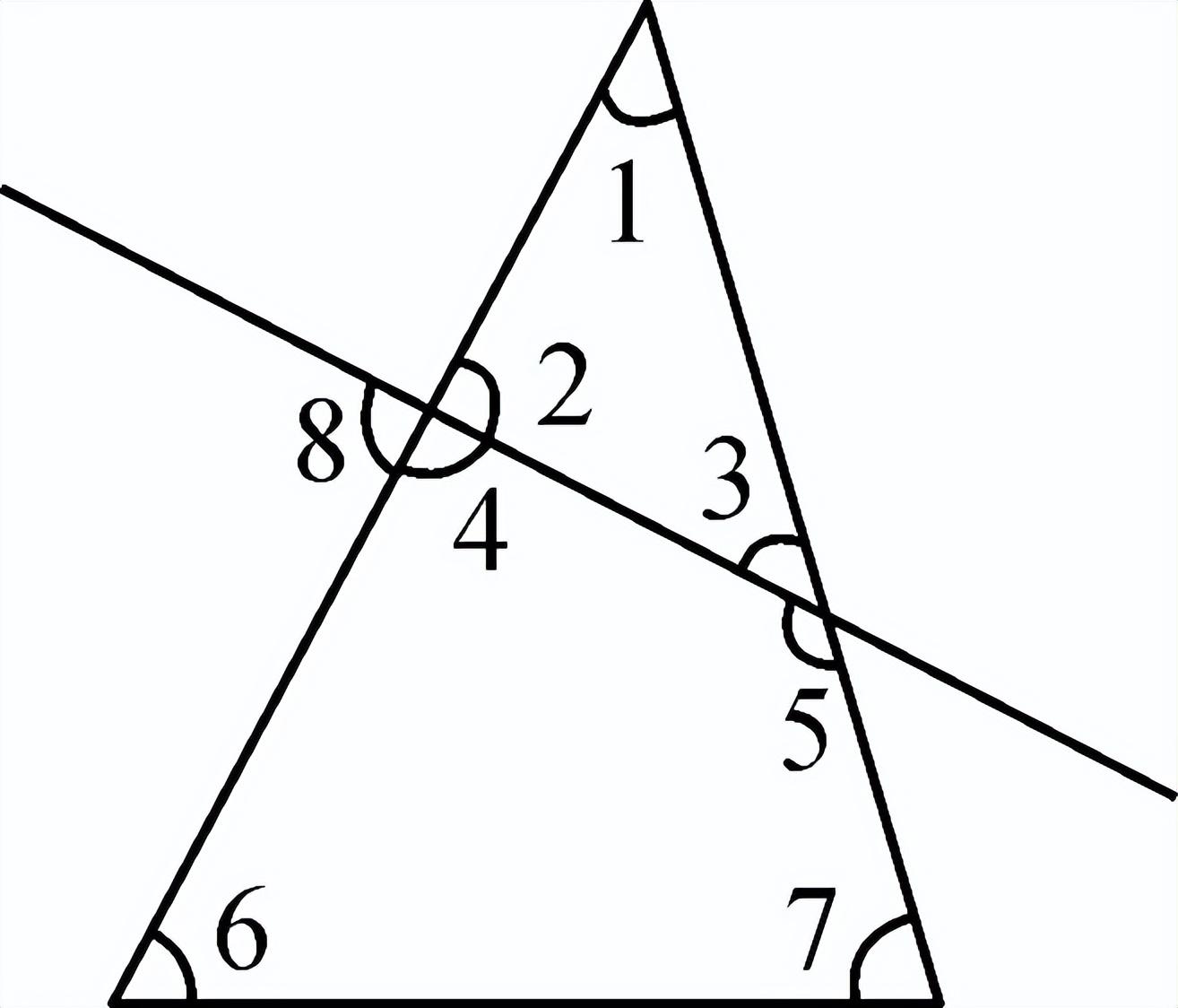 ,第6题图) 5.如图,∠1和∠2是__同位__角,∠5和∠6是__内错__角,∠2和∠6是__同旁内__角. 6.如图,下列判断错误的是( C ) A.∠1与∠2是同旁内角 B.∠3与∠4是内错角 C.∠5与∠6是同旁内角 D.∠5与∠8是同位角 四、总结梳理 内化目标 回顾本节课学习内容,请回答下列问题: 1.“三线八角”中,判断同位角、内错角、同旁内角的三个步骤: 一看角的顶点;二看角的两边;三看角的方位.这“三看”离不开主线“截线”的确定. 2.遇到较复杂的图形,可以从分解图形入手,把复杂图形化为若干个基本图形. 3.数学思想:化归思想,辩证思想. 五、达标检测 反思目标 1.如图,∠1与∠2是__内错__角,是直线__AB__和直线__BC__被直线__AC__所截而成的,∠1与∠3是__同旁内__角,是直线__AC__和直线__BC__被直线__AB__所截而形成的. 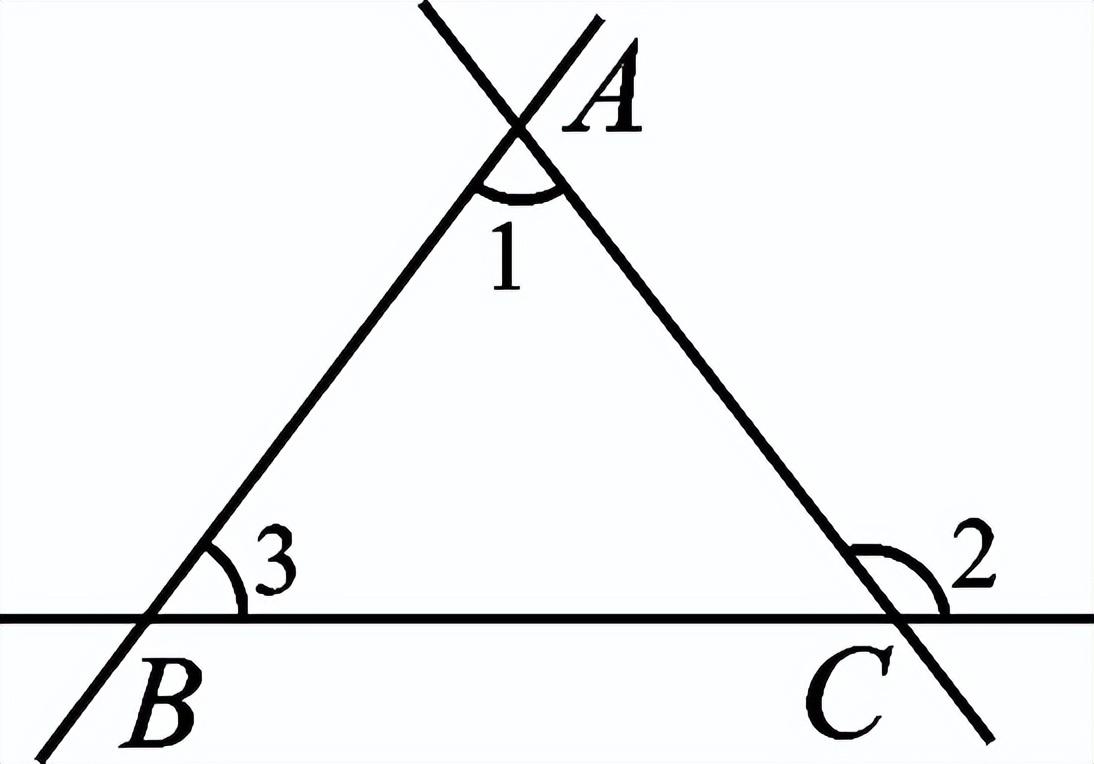 第1题图 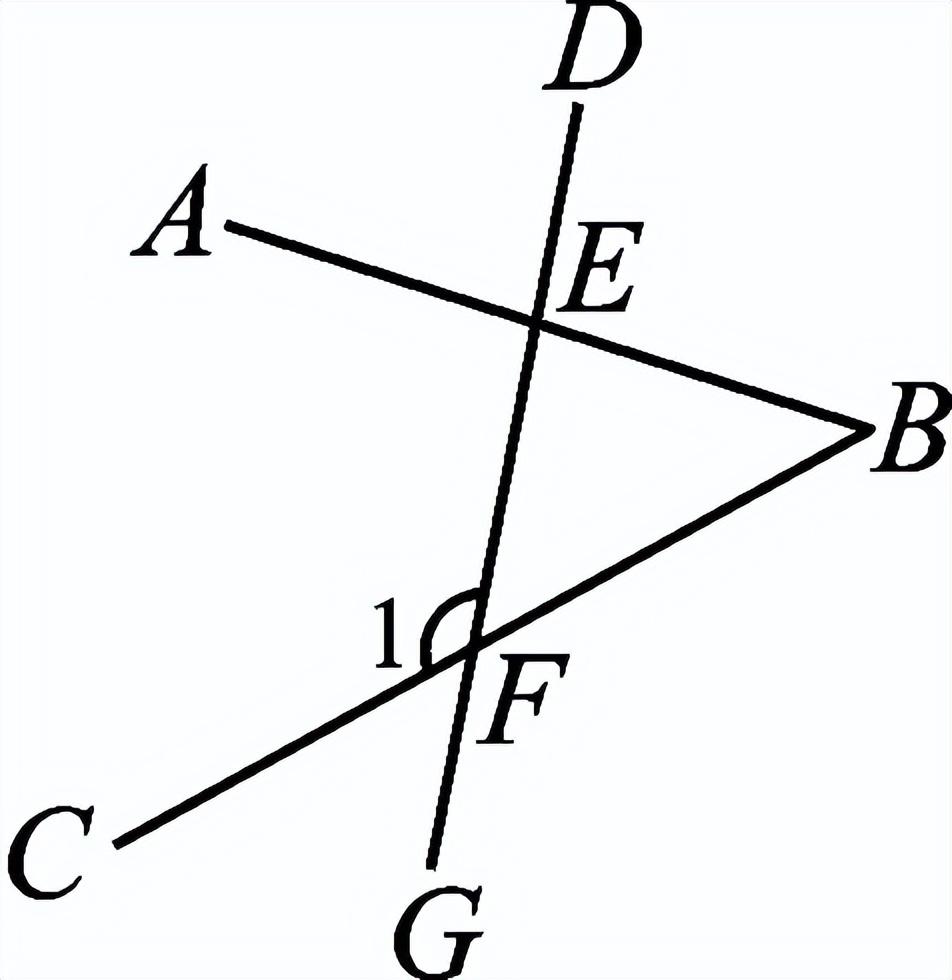 第2题图 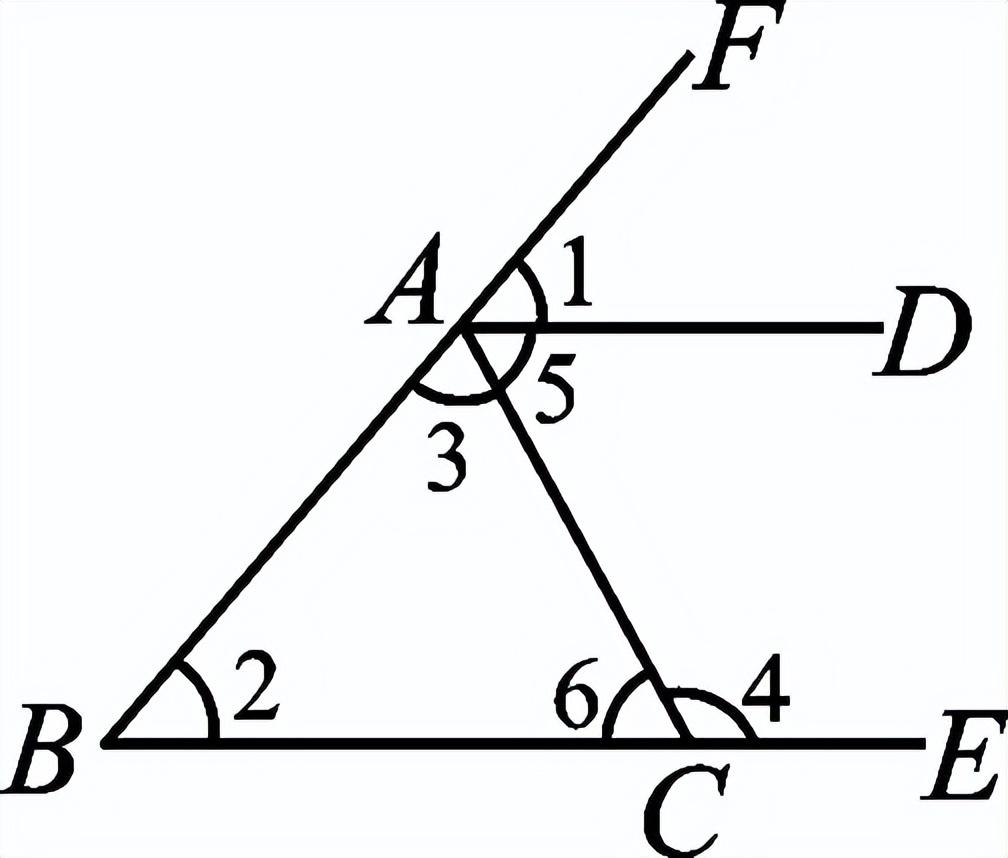 第3题图 2.如图,已知AB、CB被DG截于E、F两点,则∠1的同位角是__∠AED__,∠1的内错角是__∠BEF__,∠1的同旁内角是__∠AEF__,∠1的对顶角是__∠BFG__,∠1的邻补角是__∠EFB、∠CFG__. 3.如图,(1)∠1与∠2是__同位__角,是直线__AD__和直线__BE__被直线__BF__所截而形成的. (2)∠5与∠6是直线__AD__和直线__BE__被直线__AC__所截而形成的__内错__角. (3)∠2的同位角有__∠1、∠4和∠FAC__,∠2的同旁内角有__∠3、∠6和∠BAD__. 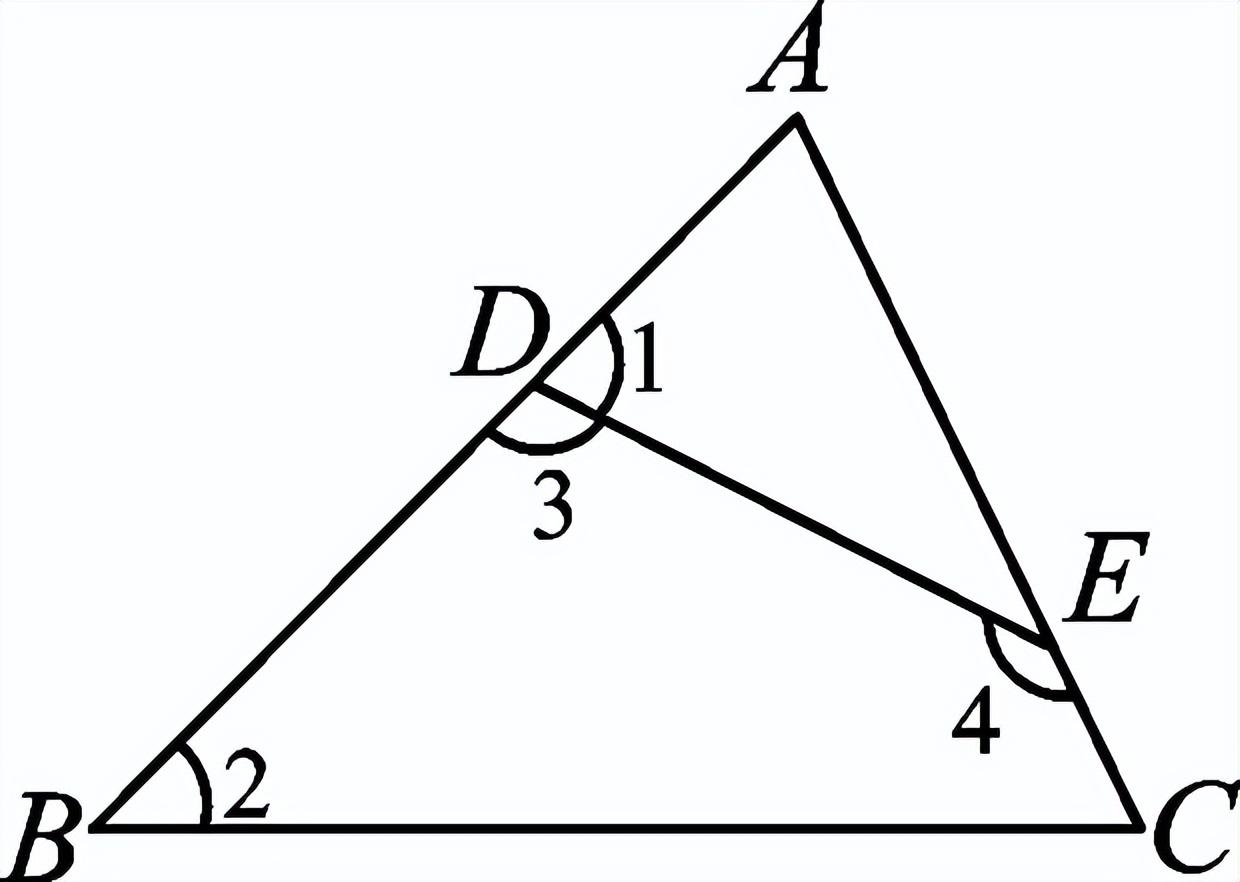 4.如图,∠1与∠2,∠3与∠4,∠1与∠4分别是哪两条直线被哪一条直线所截形成的什么角? 解:∠1与∠2是由DE,BC被AB所截得的同位角,∠3与∠4是由AB,AC被DE所截得的同旁内角,∠1与∠4是由AB,AC被DE所截得的内错角. | |||||
相关文章:
余额分期是什么意思(信用卡分期里那些不划算的事儿)06-07
车分期有什么条件(买车可以分期付款吗?)06-06
为什么会有物业费(物业费是从哪里来的?)05-09
真石漆为什么不干了(建筑外墙贴瓷砖与真石漆哪个好?)05-08
什么美缝剂好不变色(美缝用什么材料好?)05-07
